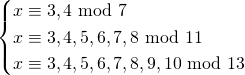Opgave 19

A mathematician, like a painter or a poet, is a maker of patterns. If this patterns are more permanent than theirs, it is because they are made with ideas ….. The mathematician’s patterns, like the painter’s or the poet’s, must be beautiful; the ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics.

T

Wiskundig denken

Geplaatst op 1 februari 2017 door admin

Wiskundig denken is de kern en de kracht van wiskunde

Wat is nu dat wiskundig denken? De Nederlandse wiskundige P.Drijvers geeft volgende omschrijving:

Bedenken hoe je wiskundig gereedschap kan gebruiken om een probleem op te lossen.

Hoe? : hier bedoelen we de keuze van de gereedschappen die je gaat gebruiken, in welke volgorde je dat doet en onder welke voorwaarden ze zinvol kunnen gebruikt worden.
Wiskundig gereedschap? : dit moet breed worden opgevat. het kan heel specifiek en concreet zijn, zoals de formule van Pythagoras, maar ook theoretisch ( logisch redeneren, bewijzen), of algemeen van karakter ( het ontwikkelen van strategieën).
Gebruiken? : niet allen het toepassen van een bestaande, kant-en-klare methode, maar ook het ontwikkelen ervan, of het op maat maken van een bestaande methode voor een specifiek doel.
Probleem? : dit is niet zomaar een opgave, maar wel een vraag waar je geen kant-en-klare oplosmethode ter beschikking hebt

Je kan drie kernaspecten beschouwen: probleemoplossen, modelleren en abstraheren.

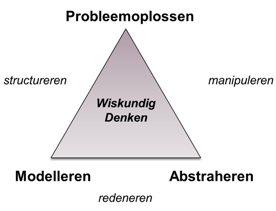
Wat voor iemand een probleem is, dus wat niet standaard is voor hem of haar, hangt af van voorkennis en ervaring. Wiskundig denken is dus relatief: wat voor de ene uitdagend en nieuw is, zal voor de andere routinematige reproductie zijn.

Wiskunde is leuk

Tag archieven: wiskunde

Opgave 19

Controleer voor elk natuurlijk getal vanaf 7 of ${n} \choose {7}$ deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.

Opgave 18

$n \in \mathbb{N}_0$ is p-veilig ( met p een natuurlijk getal verschillend van 0), als het in absolute waarde meer dan 2 verschilt van alle p-vouden. Hoeveel natuurlijke getallen bestaan er die kleiner zijn dan 10000 en tegelijkertijd 7- veilig, 11-veilig en 13-veilig zijn?

Opgave 17

Er bestaat een punt P binnen een gelijkzijdige driehoek ABC zodat |PA|= 3, |PB|=4 en |PC|=5. Bereken de lengte van de zijde van die gelijkzijdige driehoek.

Wiskunde moet mooi zijn

Wiskundig denken

Wiskundig denken is de kern en de kracht van wiskunde

Controleer voor elk natuurlijk getal vanaf 7 of deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.

is p-veilig ( met p een natuurlijk getal verschillend van 0), als het in absolute waarde meer dan 2 verschilt van alle p-vouden. Hoeveel natuurlijke getallen bestaan er die kleiner zijn dan 10000 en tegelijkertijd 7- veilig, 11-veilig en 13-veilig zijn?

Er bestaat een punt P binnen een gelijkzijdige driehoek ABC zodat |PA|= 3, |PB|=4 en |PC|=5. Bereken de lengte van de zijde van die gelijkzijdige driehoek.

Wiskundig denken is de kern en de kracht van wiskunde

Controleer voor elk natuurlijk getal vanaf 7 of ${n} \choose {7}$ deelbaar is door 12 en bereken de fractie van dergelijke getallen. Zoek de limiet van die fractie als je steeds meer getallen controleert.

$n \in \mathbb{N}_0$ is p-veilig ( met p een natuurlijk getal verschillend van 0), als het in absolute waarde meer dan 2 verschilt van alle p-vouden. Hoeveel natuurlijke getallen bestaan er die kleiner zijn dan 10000 en tegelijkertijd 7- veilig, 11-veilig en 13-veilig zijn?