Wiskunde is leuk

Nootje 43

Geplaatst op 24 december 2023 door admin

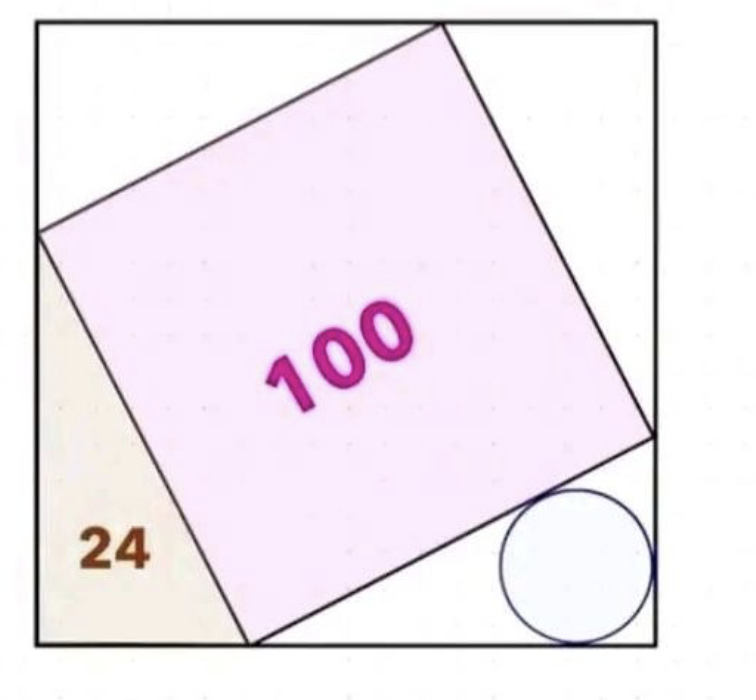
Zoek de oppervlakte van de getekende cirkel.

Antwoord

Noem de rechthoekzijden van de rechthoekige driehoeken a en b.
Dan is $a*b=2*24=48$ .
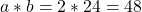De totale oppervlakte van het grote vierkant is 100 plus vierkeer de rechthoekige driehoek met oppervlakte 24, dus 196. Bijgevolg is de zijde van het grote vierkant gelijk aan 16. Dus is $a+b=16$
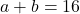
Uit de twee betrekkingen met a en b vinden we dan dat 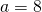$a=8$ en $b=6$ .
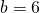Nu weten we dat de oppervlakte van een rechthoekige driehoek gelijk is aan de straal van de ingeschreven cirkel vermenigvuldigd met de halve omtrek van de driehoek. Bijgevolg is de straal gelijk aan 2.
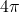De oppervlakte van de getekende cirkel is $4\pi$ .

Vierkanten en rechthoeken op een schaakbord

Geplaatst op 26 juni 2019 door admin

Hoeveel vierkanten en rechthoeken kan men vormen op een n x n schaakbord?

Nemen we eerst het aantal vierkanten. We noteren V(n) voor het aantal vierkanten dat je kan tekenen op een nxn bord. Voor de 1×1 vierkanten heb je n mogelijke verticale posities en n horizontale, dus $n^2$ mogelijke vierkanten. Voor de 2×2 vierkanten heb je n – 1 verticale en horizontale mogelijke plaatsingen , dus $(n-1)^2$ mogelijkheden. Uiteindelijk is het totaal aantal vierkanten gelijk aan $n^2+(n-1)^2+\cdots+2^2+1^2$ .
$V(n)=\frac{n(n+1)(2n+1)}{6}$
Met R(n) noteren we het aantal rechthoeken dat je kant tekenen op een nxn schaakbord. Voor een rechthoek heb je 2 verticale en twee horizontale lijnen nodig. Er zijn n+1 verticale en n+1 horizontale lijnen op een schaakbord. Om de verticale lijnen te kiezen heb je dus ${n+1}\choose{2}$ $=\frac{n(n+1)}{2}$ mogelijkheden. Idem voor de keuze van de twee horizontale lijnen. Dus
$R(n)=\frac{n^2(n+1)^2}{4}$
Voor een 8×8 schaakbord heb je dus 204 vierkanten en 1296 rechthoeken. Van die rechthoeken zijn er 1092 die geen vierkant zijn.