Schrijf in Python een programma dat zelf een getal kiest tussen 1 en 100. Jij moet raden welk getal het is. de computer geeft enkel aan of je lager of hoger moet gokken.
Een paar opmerkingen:
Een mogelijke output :
Neem een willekeurig getal, zeg 56 en vermenigvuldig de cijfers. dan bekom je 5*6=30. Bij dit getal neem je opnieuw het product van de cijfers: 3*0=0. Als je nu verder zou gaan met het product van de cijfers te nemen, dan verandert er niets meer. Na 2 stappen bekom je dus een getal van 1 cijfer. We noemen 2 de volhardingswaarde van het gegeven getal 56.
Algemeen: Neem dus een willekeurig getal, vermenigvuldig alle cijfers met elkaar, zodat je een nieuw getal krijgt. Als dat getal meerdere cijfers bevat, herhaal je het proces van cijfers vermenigvuldigen, totdat je maar 1 cijfer over houdt. Het aantal stappen dat je daarvoor nodig hebt noem je de volhardingswaarde van het gegeven getal.
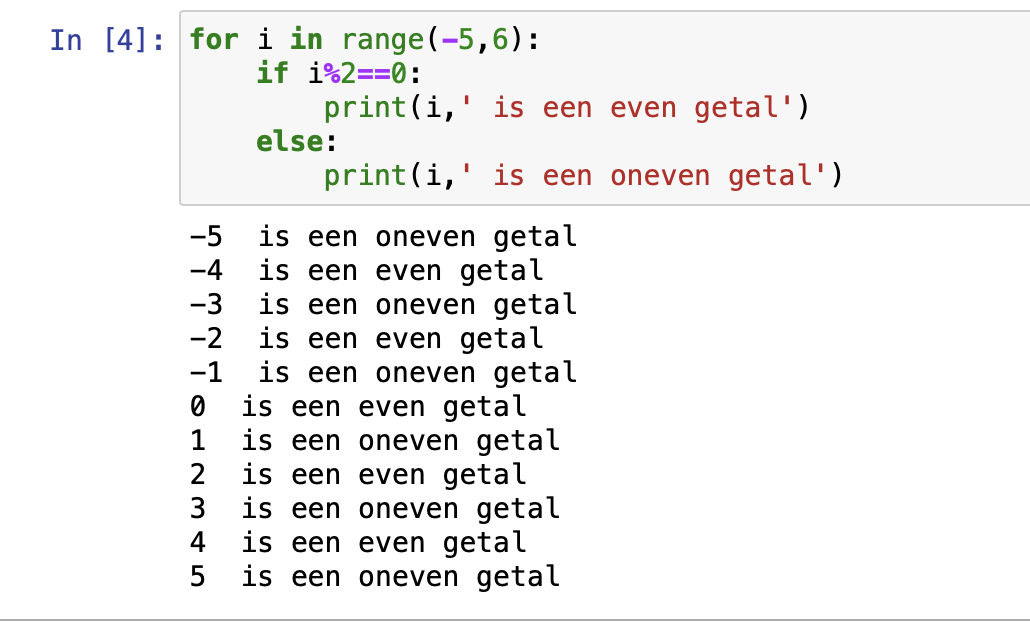
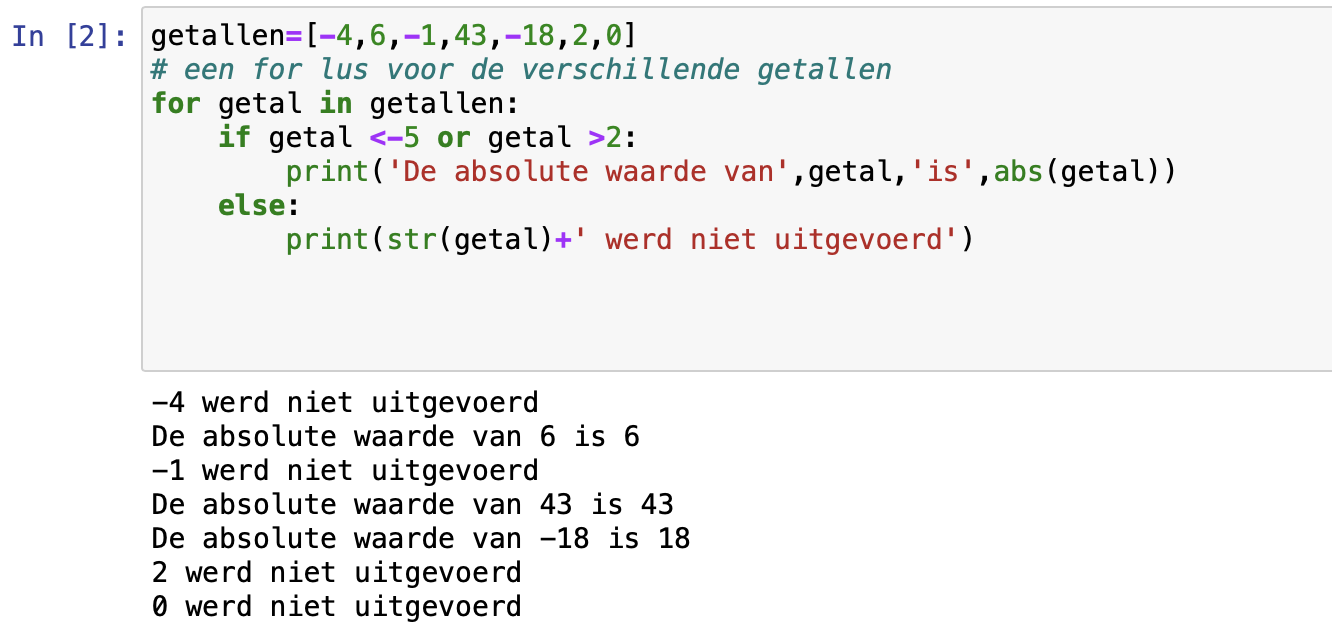
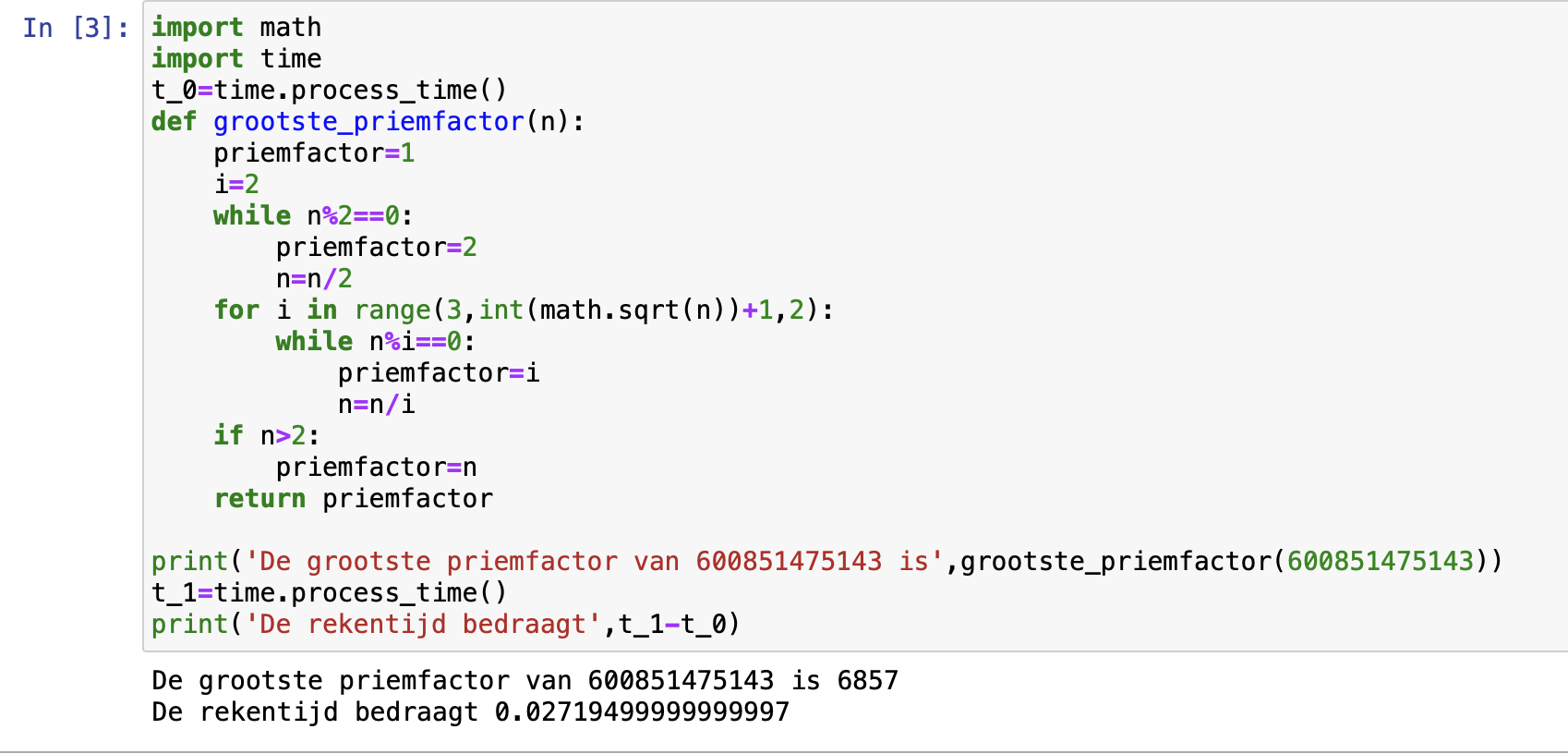
Een programma in Python:
Is er een maximaal aantal stappen voor een willekeurig getal? Dit ‘eenvoudig’ probleem werd bedacht door Neil Sloane, een Amerikaanse wiskundige.
We kennen hem het best van zijn website (oeis.org) met zijn verzameling getallenreeksen. In 1973 schreef hij in Journal of Recreational Mathematics een artikel over het probleem van de volhardingswaarde. Hij beweerde dat we maximaal 11 stappen kunnen maken eer we een enkel cijfer over houden, hoe groot het begin getal ook is. Dit vermoeden werd tot op heden nog niet bewezen.
Het kleinste getal met volhardingswaarde 1 is uiteraard 10. Verder is 25 het kleinste getal met volhardingswaarde 2, 39 het kleinste getal met volhardingswaarde 3, 77 het kleinste getal met volhardings-waarde 4 en 679 het kleinste getal met volhardingswaarde 5.
De kleinste getallen met volhardingswaarden 6,7,8,9,10 en 11 zijn respectievelijk 6788,68889,2677889,26888999,3778888999 en 277777788888899.
Een deling in Python:
Een mooie toepassing is van een reeks getallen nakijken of ze even zijn of niet. Even getallen geven rest 0 bij deling door 2:
