Tag archieven: complexe getallen

Opgave 31

Geplaatst op door

Het getal 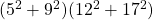(5^2+9^2)(12^2+17^2) kan geschreven worden als som van twee kwadraten van positieve gehele getallen. Geef zo een schrijfwijze.

Antwoord

  • We zouden de vraag algemener kunnen stellen: schrijf (a^2+b^2)(c^2+d^2) als som van twee kwadraten.
  • Het is gemakkelijk aan te tonen dat dit product gelijk is aan (ac+bd)^2+(ad-bc)^2 of (ac-bd)^2+(ad+bc)^2.
  • Zo vinden we dat (5^2+9^2)(12^2+17^2)=93^3+193^3=213^2+23^2.
  • Je kan de oplossing ook vinden door gebruik te maken van complexe getallen.
  • Zo is 5^2+9^2 het kwadraat van de modulus van 5+9i.
  • Omdat de modulus van een product gelijk is aan het product van de moduli is (5^2+9^2)(12^2+17^2) het kwadraat van de modulus van o.a. (5+9i)(12+17i)=-93+193i. Zo bekom je hetzelfde resultaat.

 

 

Gehelen van Gauss

Geplaatst op door

Gehelen van Gauss zijn complexe getallen a+bi waarbij a en b gehelen getallen zijn. Je kan ze optellen en vermenigvuldigen. Zo vormen ze een interessante structuur : een commutatieve ring met eenheidselement. In deze tekst worden de basisbegrippen van de ringtheorie, aan de hand van de ring van de gehelen van Gauss, besproken. Zo bespreken we de eenheden, de priem elementen en de idealen van deze ring. Geen bewijzen , maar alle interessante begrippen komen aan bod. De lezer kan ze nadien zelf uitwerken. In onderstaande afbeelding vind je bijvoorbeeld alle priem elementen in het vlak van Gauss.

priem

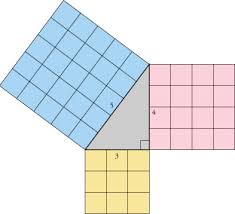
Pythagorese drietallen en complexe getallen

Geplaatst op door

Een Pythagorees drietal is een drietal positieve gehele getallen (a,b,c) waarvoor geldt dat a^2+b^2=c^2. Zo is (3,4,5) een Pythagorees drietal omdat 3^2+4^2=5^2. De naam komt van de stelling van Pythagoras, aangezien dergelijke getallen kunnen optreden als de zijden van een rechthoekige driehoek met c als lengte van de schuine zijde.

piet

Een Pythagorees (a,b,c)  drietal heet primitief als de grootste gemene deler van a,b en c gelijk is aan 1. Zo is (3,4,5) primitief , maar ( 6,8,10) niet.

Wat hebben complexe getallen hiermee nu te maken? Neem een complex getal z = a+ bi met a en b geheel. We spreken dan van een complex geheel getal.  Definieer de norm N(z) van het complex getal als N(z) = a^2+b^2. Het is duidelijk dat de norm multiplicatief is, m.a.w. N(z.w)=N(z).N(w). Maar dan is

    \[N(z^2)=(N(z))^2\]

De betrekking a^2+b^2=c^2 kan je dus herschrijven als N(z)=c^2 met z=a+bi. We zijn dus op zoek naar complexe gehele getallen waarvan de norm een volkomen kwadraat is. Maar bovenstaande formule leert ons dat de norm van een complex getal een volkomen kwadraat is als het zelf een volkomen kwadraat is. Om een Pythagorees drietal te construeren, nemen we dus een willekeurig complex geheel getal en kwadrateren we dit getal. Dit kwadraat zal een complex getal  zijn a+bi zijn, waarvan de  norm N(a+bi)=a^2+b^2 een volkomen kwadraat is.

Neem bijvoorbeeld het complex getal 2+i. Dan is (2+i)^2=4+4i+i^2=3+4i. De norm van dit kwadraat is 3^2+4^2=25 . Hiermee correspondeert het Pythagorees drietal ( 3,4,5).

Vertrekken we algemeen van het complex geheel getal z=x+yi. Kwadrateren we z:  (x+yi)^2=x^2-y^2+2xyi. De norm hiervan is (x^2-y^2)^2+4x^2y^2=(x^2+y^2)^2 Zo krijgen we de gekende formule voor een willekeurig Pythagorees drietal

    \[(x^2-y^2,2xy,x^2+y^2)\]

Als  x en y onderling ondeelbaar zijn , dan is het zo gevormde  Pythagorees drietal primitief. Bijgevolg hebben we aangetoond dat met deze constructie via kwadraten van complexe gehele getallen x+yi met x en y onderling ondeelbaar, elk primitief Pythagorees drietal kan worden verkregen.