Op hoeveel manieren kan je een rijtje van 10 symbolen 0,1 of 2 maken zodat er nooit twee enen of twee twee na elkaar voorkomen?
Goed is dus 1200121001 en fout is 0012011202 omdat hier twee enen na elkaar voorkomen.
Vorm de matrix
![Rendered by QuickLaTeX.com \[A=\begin{pmatrix} 1&1&1\\1&0&1\\1&1&0\end{pmatrix}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a4300b75ff59bfd65e863df8763b10b5_l3.png)
Nummer de rijen en de kolommen met 0,1en 2
![]() betekent: er is een mogelijkheid om na een 0 een tweede nul te plaatsen.
betekent: er is een mogelijkheid om na een 0 een tweede nul te plaatsen.![]() betekent : na een 1 kan er geen 1 komen.
betekent : na een 1 kan er geen 1 komen.![]() betekent: na een 1 kan er een 2 komen.
betekent: na een 1 kan er een 2 komen.
Het is duidelijk dat de som van de elementen van deze matrix A het aantal goede tweetallen is: 00,01,02,10,12,20,21 . Er zijn 7 goede tweetallen.
Net zoals bij een directe wegenmatrix (soort overgangsmatrix) zal de som van de elementen van ![]() dan het aantal goede tientallen geven:
dan het aantal goede tientallen geven:
![Rendered by QuickLaTeX.com \[A^9=\begin{pmatrix} 1393&985&985\\985&696&697\\985&697&696\end{pmatrix}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b1cac41c15a3ff2ff22e58a337790479_l3.png)
Het antwoord op de gestelde vraag is dan 8119.

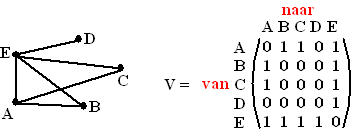




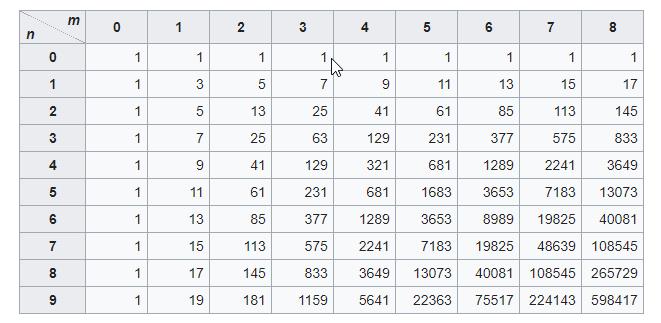

![Rendered by QuickLaTeX.com \[\sum_{k=0}^{ min(m,n)}\dfrac{(m+n-k)!}{k! (m-k)! (n-k)!}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-3ccd7347c9ba955bb4a8b994358c565f_l3.png)