Een cirkel van Apollonius is de meetkundige plaats in het vlak van alle punten p, die bij gegeven punten A en B, voldoen aan
![Rendered by QuickLaTeX.com \[d(P,A)=r . d(P,B)\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-e804155a5384d5958f5d782d81fb7d08_l3.png)
De naam van deze cirkel komt van de Griekse astronoom en wiskundige Apollonius van Perga( 262-190 BC). Hij was degene die kegelsnedes, zoals ellipsen, parabolen en hyperbolen, de namen gaf die we tot op de dag van vandaag nog gebruiken. Zijn achtdelige ”Konika” over kegelsnedes wordt gezien als één van de grootste werken uit de antieke meetkunde. Verder heeft hij enorm bijgedragen aan de astronomie. Dit blijkt uit de, naar hem vernoemde, Apolloniuskrater op de maan.

Merk eerst en vooral op dat als r = 1, dat de meetkundige plaats een rechte is, namelijk de middelloodlijn van ![Rendered by QuickLaTeX.com \left[A,B\right]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-1df1ffc8845ed73cee73275553d25593_l3.png) .
.
Veronderstel nu dan dat 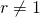 . Als we de oorsprong in A leggen, de X-as door A en B en B(d,0) noemen, dan is de nodige en voldoende voorwaarde voor (x,y) om op de meetkundige plaats te leggen gegeven door
. Als we de oorsprong in A leggen, de X-as door A en B en B(d,0) noemen, dan is de nodige en voldoende voorwaarde voor (x,y) om op de meetkundige plaats te leggen gegeven door 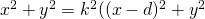 . Na wat rekenwerk is dit te herleiden tot
. Na wat rekenwerk is dit te herleiden tot
![Rendered by QuickLaTeX.com \[\big(x-\dfrac{k^2d}{k^2-1}\big)^2+y^2=\dfrac{k^2d^2}{(k^2-1)^2}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-33ef5f38254cac82c4d01482fd86c389_l3.png)
Dit is inderdaad een cirkel met middelpunt
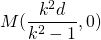
en straal
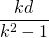
.
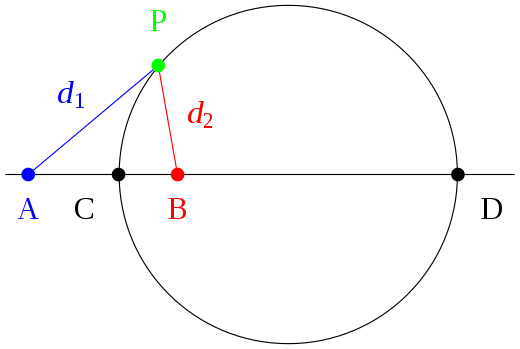
Als C en D de snijpunten zijn van de cirkel met de X-as, dan geldt voor elk punt P van de cirkel dat PC en PD de deellijnen zijn van de driehoek ABP. In een driehoek worden, vanwege deze eigenschap, de cirkels door een hoekpunt en door de snijpunten van de bissectrices door dat hoekpunt met de overstaande zijde de cirkels van Apollonius van die driehoek genoemd.
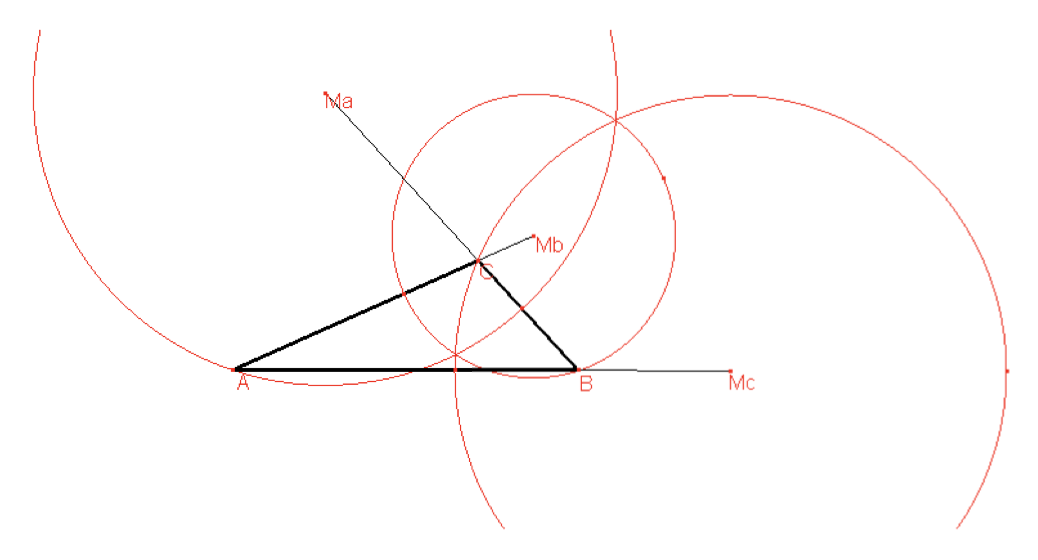
Een paar opmerkingen:
- De Apollonius cirkel door A heeft als verhouding
 .
.
- Elk van deze cirkels staat loodrecht op de omgeschreven cirkel van de driehoek.
- De middelpunten van de drie cirkels liggen op één lijn.
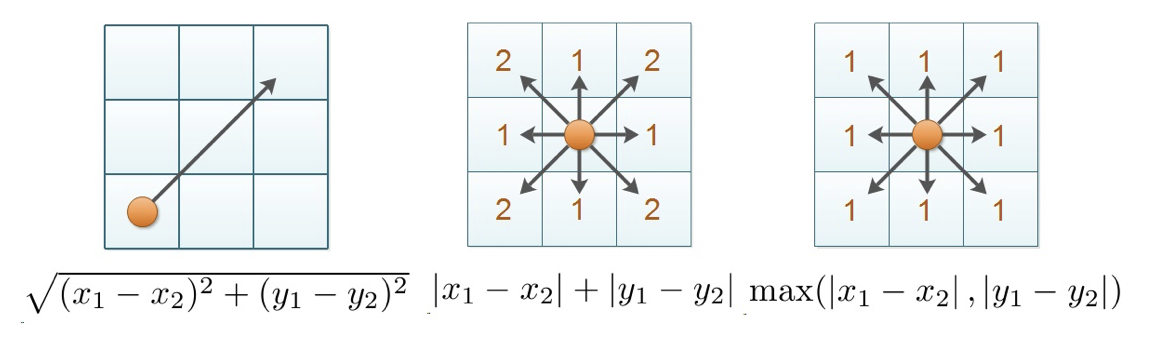
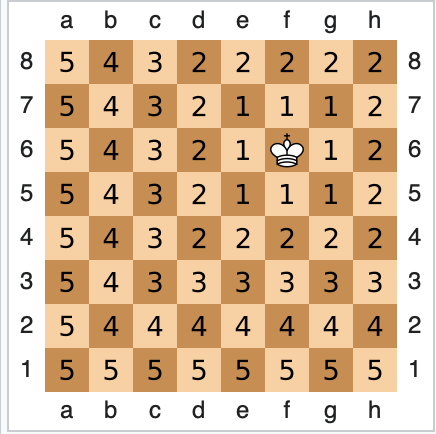
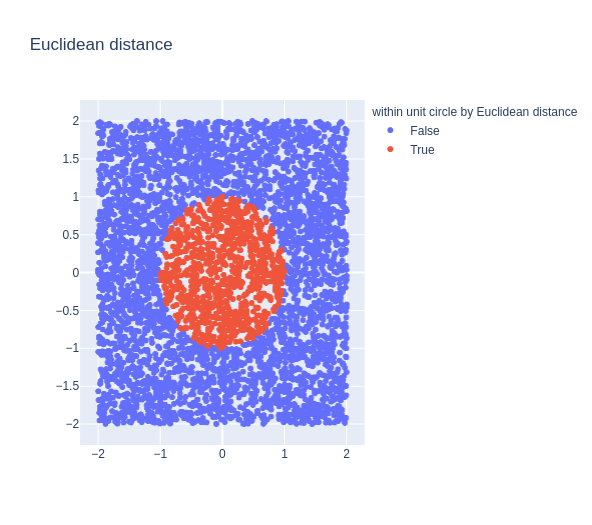
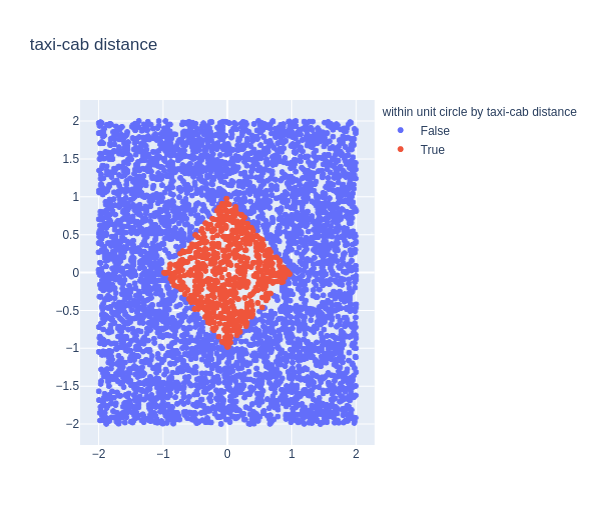
![]() en
en ![]() , dan is de Chebychev afstand het maximum van de getallen
, dan is de Chebychev afstand het maximum van de getallen ![]() en de taximetrische afstand is de som van al die getallen.
en de taximetrische afstand is de som van al die getallen.