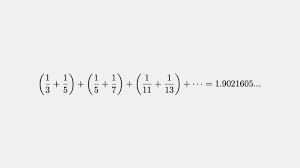Nootje 34

Geplaatst op door

Bereken de som van de coëfficiënten van de veelterm P(x) als

    \[(10x^{34}+2x^3+5)P(x)=2023x^{2023}\]

Antwoord

  • Het is handig te weten dat de som van de coëfficiënten van een veelterm kan berekend worden door de getalwaarde van 1 te berekenen, dus P(1).
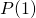  • Vullen we 1 in bij de gegeven identiteit, dan vinden we: (10+2+5)P(1)=2023;
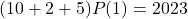  • Hieruit volgt dat P(1)=119
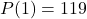
  • De som van de coëfficiënten van de veelterm Px) is dus 119.

Nootje 33

Geplaatst op door

Vind x-y als gegeven is dat x^4=y^4+24, x^2+y^2=6 en x+y=3.

Antwoord

  • Om de 2 onbekenden x en y uit te rekenen heb je eigenlijk maar 2 vergelijkingen nodig. Dan kan je ook x-y uitrekenen. Maar waarschijnlijk is dat wel niet de bedoeling.
  • Omdat x^4-y^4=(x-y)(x+y)(x^2+y^2), vinden we uit de eerste betrekking dat 24=(x-y)*3*6;
  • Hieruit volgt dan dat x-y=\frac{4}{3}.

De gulden snede en de rij van Fibonacci

Geplaatst op door

We kennen allemaal de gulden snede. Bij de gulden snede verhoudt het grootste van de twee delen van een lijnstuk zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. 

Maar er is ook een verband tussen \varphi en de rij van Fibonacci. Noteren we het n-de getal in deze rij door F(n).

  • Als we in bovenstaande uitdrukking \frac{a}{b} vervangen door \varphi, dan vinden we dat \varphi^2=\varphi+1.
  • Maar dat is \varphi^3=\varphi^2+\varphi=2\varphi+1.
  • Dus \varphi^4=2\varphi^2+\varphi=3\varphi+2.
  • Algemeen kan men dan stellen dat :

        \[\varphi^n=F(n)\varphi+F(n-1)\]

De constante van Brun

Geplaatst op door

Vrij veel priemgetallen zijn twee opeenvolgende oneven getallen, zoals 3 en 5 of 17 en 19. Of er oneindig veel zulke paren, priemtweelingen genoemd, zijn is niet bewezen .

In 1919 bewees de Noorse wiskundige Viggo Brun( 1885-1978) volgende eigenschap:de som van de omgekeerde waarden van de priemtweelingen nadert tot een bepaalde waarde, die nu de constante van Brun wordt benoemd.

  • Het is merkwaardig dat deze som begrensd is terwijl de som van de omgekeerden van alle priemgetallen oneindig groot is. Dit laat vermoeden dat het priemtweelingen eerder schaars zijn.
  • Het is onbekend of de constante van Brun een irrationaal getal is. Dit hangt ervan af of het aantal priemtweelingen eindig of oneindig is.

  • Een schatting van Pascal Sebah en Patrick Dechimel in 2002 die alle priemtweelingen tot 1016 gebruikt komt op B  ≈ 1,902160583104.