Enkele leerlingen van 4NAWE B van de Prins in Diest hebben zich gewaagd aan een ‘wiskundige’ haiku. De eerste komt van Lars Nies en de tweede van Mathieu De Busser:
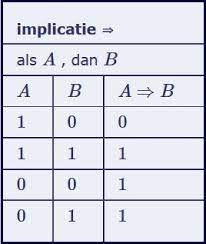
Waarheidstabel rolt
logische keuzes maken
leugen of waarheid
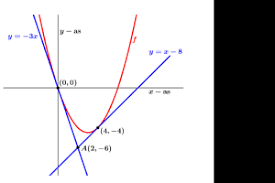
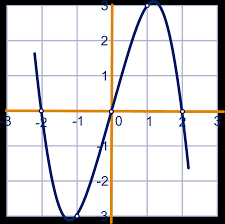
Berg of dal in beeld
tweedegraads is altijd leuk
x is er altijd