N is een natuurlijk getal. Een goede verdeling van N is een partitie van ![]() in twee gescheiden, niet lege deelverzamelingen
in twee gescheiden, niet lege deelverzamelingen ![]() en
en ![]() , zo dat de som van de elementen van
, zo dat de som van de elementen van ![]() gelijk is aan het product van de elementen van
gelijk is aan het product van de elementen van ![]() . Bewijs dat voor
. Bewijs dat voor ![]() er altijd een goede verdeling bestaat.
er altijd een goede verdeling bestaat.
Spoiler
- Laten we eerst even op verkenning gaan en kijken of we een goede verdeling vinden voor 5,6 en 7.
- Voor 5 vinden we
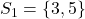 en
en 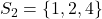 .
. - Voor 6 vinden we
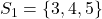 en
en 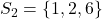 .
. - Voor 7 vinden we
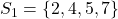 en
en 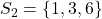 .
. - In deze voorbeelden vinden we
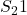 van de vorm
van de vorm 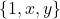 . Proberen we eens of dit altijd kan!
. Proberen we eens of dit altijd kan! 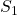 is het complement van
is het complement van 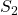 dus we krijgen een goede verdeling als
dus we krijgen een goede verdeling als ![Rendered by QuickLaTeX.com \[\frac{N(N+1)}{2}-1-x-y=xy\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-7edae9fc9c6e8a80a67747293e461910_l3.png)
- Uitgewerkt geeft dit
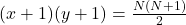 .
. - Als nu
 en N even is , dan kunnen we voor x en y volgende oplossingen vinden:
en N even is , dan kunnen we voor x en y volgende oplossingen vinden: ![Rendered by QuickLaTeX.com \[x=\frac{N}{2}-1 \text{ en } y=N\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-60c86b64917a33edc6de1bcb57ad6bde_l3.png)
- Als N echter oneven is, vinden we:
![Rendered by QuickLaTeX.com \[x=\frac{N+1}{2}-1 \text{ en } y=N-1\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-fd068e993a637fb117cb25f11ffad25e_l3.png)
- We hebben dus een constructie bewijs gegeven van het gevraagde.
