Als je 5 ballen moet verdelen over 4 dozen, dan zal er een doos zijn met minstens 2 ballen. Immers de eerste 4 ballen kan je nog over de 4 dozen verdelen, maar voor het 5 de balletje is er geen doos meer over. Algemeen: verdeel je meer dan n objecten over n laden, dan bevat minstens één lade minstens 2 van die objecten. Dit eenvoudig principe werd voor het eerst expliciet gebruikt door Dirichlet (1805 – 1859) en wordt daarom ook het ladenprincipe of duivenhokprincipe van Dirichlet genoemd. Het principe kan in een nog algemenere vorm gegoten worden: Als je ![]() ( met
( met ![]() en
en ![]() ) objecten verdeelt over
) objecten verdeelt over ![]() laden, dan is er minstens \’e\’en lade met minstens
laden, dan is er minstens \’e\’en lade met minstens ![]() objecten.
objecten.
Een voorbeeld:
Neem willekeurig  getallen uit de verzameling
getallen uit de verzameling 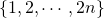 . Bewijs dat er in die
. Bewijs dat er in die  getallen steeds een getal bestaat dat deelbaar is door een ander van die
getallen steeds een getal bestaat dat deelbaar is door een ander van die  getallen.
getallen.
- Neem
 getallen en noteer die door
getallen en noteer die door 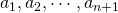 en schrijf ze in de vorm
en schrijf ze in de vorm 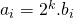 waarin
waarin 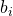 oneven is.
oneven is. - We hebben
 oneven getallen
oneven getallen 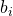 , allen uit het interval
, allen uit het interval ![Rendered by QuickLaTeX.com \left[1,2n-1\right]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-0081fc453abed64f8fcd70041b72c6b3_l3.png) .
. - In het interval
![Rendered by QuickLaTeX.com \left[1,2n-1\right]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-0081fc453abed64f8fcd70041b72c6b3_l3.png) zijn er maar
zijn er maar 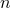 oneven getallen.
oneven getallen. - Volgens het duivenhokprincipe moeten er dus een
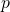 en een
en een 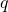 bestaan zodat
bestaan zodat 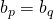 . Dan is één van de getallen
. Dan is één van de getallen 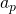 of
of 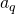 deelbaar door het andere.
deelbaar door het andere.
